2.6. Order Notation¶
Let us introduce a concise notation for asymptotic behaviour of time demand functions as an input size \(n\) of an algorithm grows infinitely, i.e., \(n \rightarrow \infty\).
2.6.1. Big O-notation¶
Definition
The positive-valued function \(f(x) \in O(g(x))\) if and only if there is a value \(x_0\) and a constant \(c > 0\), such that for all \(x \geq x_0\), \(f(x) \leq c \cdot g(x)\).
This definition can be illustrated as follows:
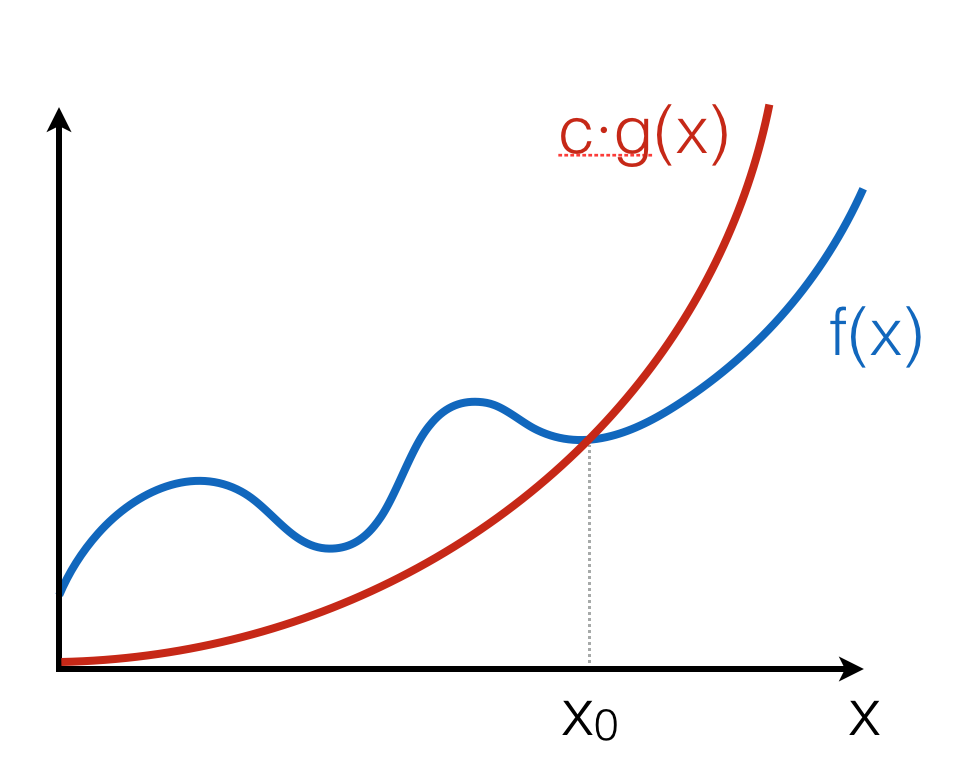
The intuition is that \(f(x)\) grows no faster than \(c \cdot g(x)\) as \(x\) gets larger. Notice that the notation \(O(g(x))\) describes a set of functions, “approximated” by \(g(x)\), modulo constant factors and the starting point.
2.6.2. Properties of Big O-notation¶
Property 1
\(O(k \cdot f(n)) = O(f(n))\), for any constant \(k\).
Multiplying by \(k\) just means re-adjusting the values of the arbitrary constant factor \(c\) in the definition of big-O. This property ensures machine-independence (i.e., we can forget about constant factors). Since \(\log_{a}n = \log_{a}b \times \log_{b}n\), we don’t need to be specific about the base when saying \(O(\log~n)\).
Property 2 \(f(n) + g(n) \in O(\max(f(n), g(n))\)
Here, \(\max((f(n), g(n))\) is a function that for any n, returns the maximum of \(f(n)\) and \(g(n))\):
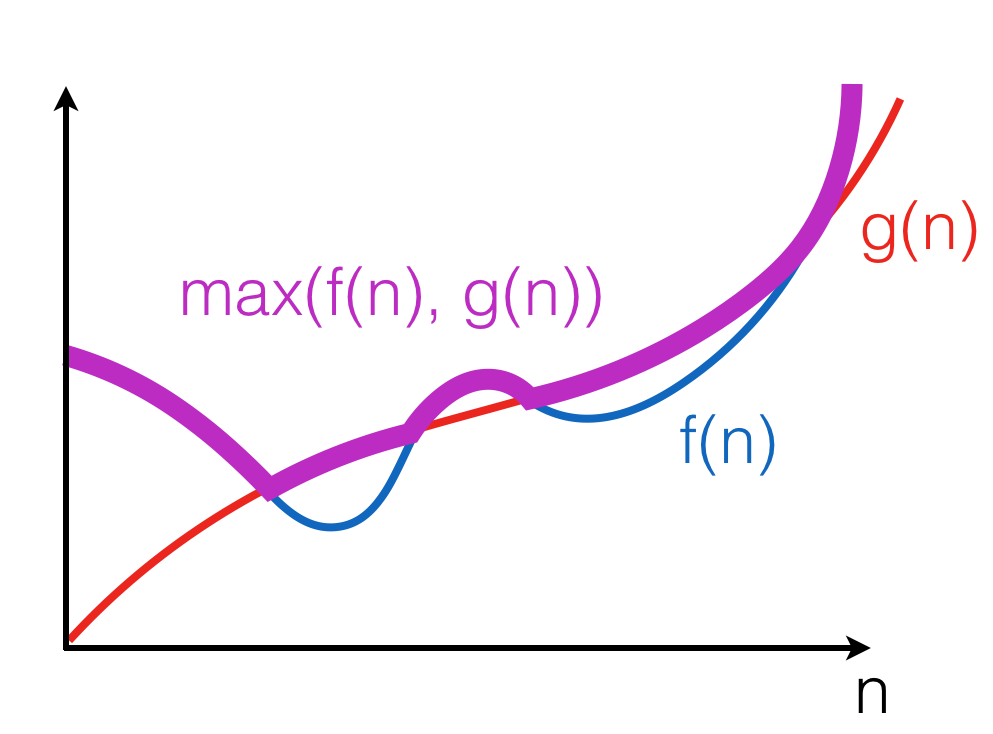
The property follows from the fact that for any \(n, f(n) + g(n) \leq 2 \cdot f(n)\) or \(f(n) + g(n) \leq 2 \cdot g(n)\). Therefore, \(f(n) + g(n) \leq 2 \cdot \max(f(n), g(n))\).
Property 3
\(\max(f(n), g(n)) \in O(f(n) + g(n))\).
This property follows from the fact that for any \(n, \max(f(n), g(n)) \leq f(n)\) or \(\max(f(n), g(n)) \leq g(n)\). Therefore, \(\max(f(n), g(n)) \leq f(n) + g(n)\).
Corollary
\(O(f(n) + g(n)) = O(\max(f(n), g(n))\).
Property 4
If \(f(n) \in O(g(n))\), then \(f(n) + g(n) \in O(g(n))\).
Follows from the fact that there exist \(c, n_0\), such that for any \(n \geq n_0, f(n) \leq c \cdot g(n)\); Therefore, for any \(n \geq n0, f(n) + g(n) \leq (c + 1) \cdot g(n)\). Intuitively, a faster-growing function eventually dominates.
2.6.3. Little o-notation¶
Definition
The positive-valued function \(f(x) \in o(g(x))\) if and only if for all constants \(\varepsilon > 0\) there exists a value \(x_0\) such that for all \(x \geq x_0, f(x) \leq \varepsilon \cdot g(x)\).
This definition provides a tighter boundary on \(f(x)\): it states that \(g(x)\) grows much faster (i.e., more than a constant factor times faster) than \(f(x)\).
Example
We can show that \(x^2 \in o(x^3)\), as for any \(\varepsilon > 0\) we can take \(x_0(\varepsilon) = \frac{1}{\varepsilon} + 1\), so for all \(x \geq x_0(\varepsilon), \varepsilon \cdot x^3 \geq \varepsilon \cdot (\frac{1}{\varepsilon} + 1) \cdot x^2 > x^2\).
2.6.4. Proofs using O-notation¶
Standard exercise: show that \(f(x) \in O(g(x))\) (or not) is approached as follows:
- Unfold the definition of O-notation;
- Assuming that the statement is true, try to find a fixed pair of values \(c\) and \(x_0\) from the definition to prove that the inequality holds for any \(x\);
- If such fixed pair cannot be found, as it depends on the value of \(x\), then the universal quantification over \(x\) in the definition doesn’t hold, hence \(f(x) \notin O(g(x))\).
Example 1: Is \(n^2 \in O(n^3)\)?
Assume this holds for some \(c\) and \(n_0\), then:
As this clearly holds for \(n_0 = 2\) and \(c = 1\), we may conclude that \(n^2 \in O(n^3)\).
\(\square\)
Example 2: Is \(n^3 \in O(n^2)\)?
Assume this holds for some \(c\) and \(n_0\), then:
Now, since \(c\) and \(n_0\) are arbitrary, but fixed, we can consider \(n = c + 1 + n_0\) (and so we can do for any \(c\) and \(n_0\)), so we see that the inequality doesn’t hold, hence in this case no fixed \(c\) and \(n_0\) can be found to satisfy it for any \(n\). Therefore \(n^3 \notin O(n^2)\).
\(\square\)
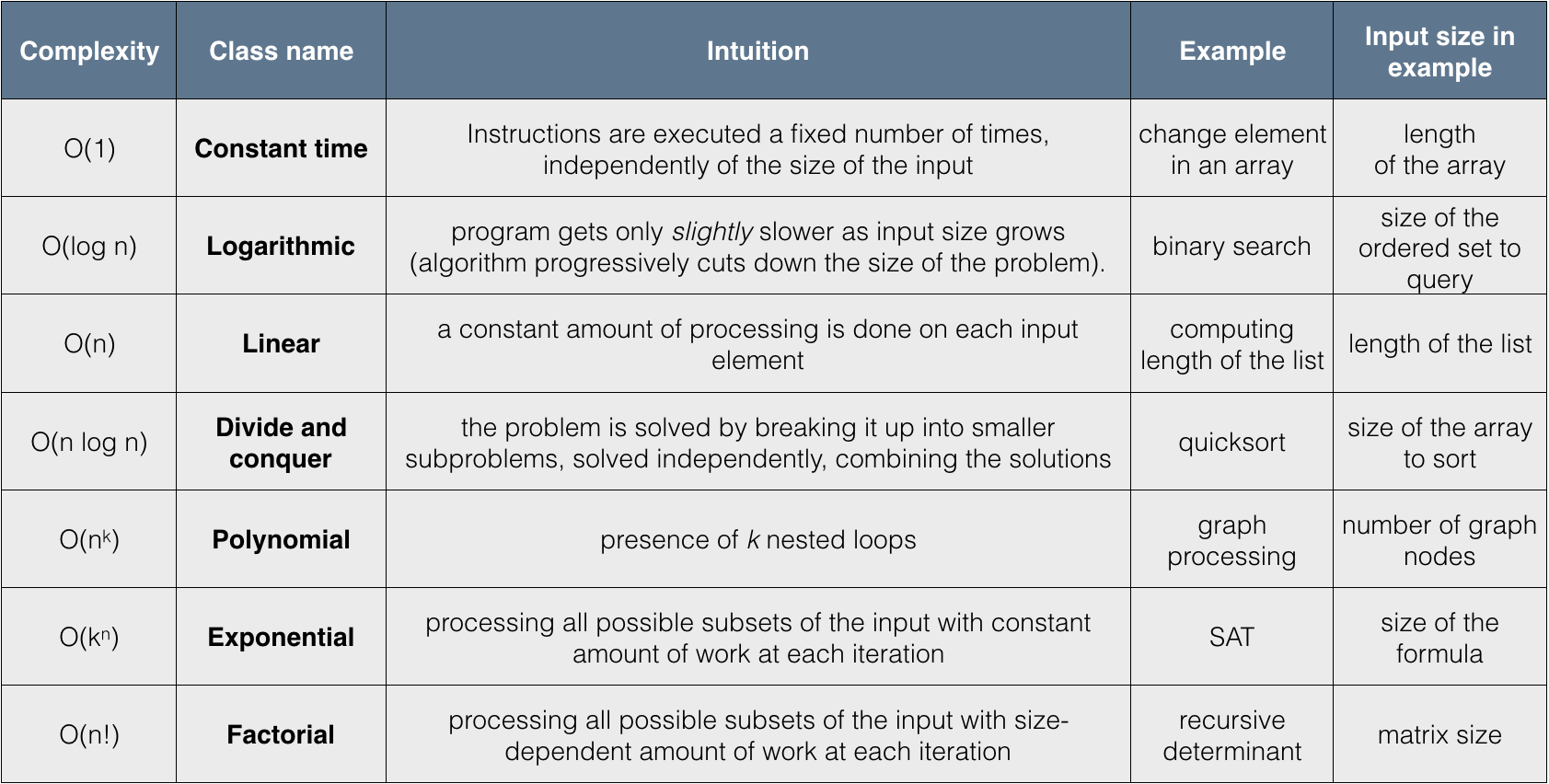
2.6.5. Hierarchy of algorithm complexities¶
2.6.6. Complexity of sequential composition¶
Consider the following OCaml program, where a is a value of size n:
let x = f1(a)
in x + f2(a)
Assuming the complexity of f1 is \(f(n)\) and the complexity of f2 is \(g(n)\), executing both of them sequentially leads to summing up their complexity, which is over-approximated by \(O(\max(f(n), g(n))\). This process of “collapsing” big O’s can be repeated for a finite number of steps, when it does not depend on the input size.
2.6.7. Exercise 6¶
Assume that each of the expressions below gives the time demand \(T(n)\) of an algorithm for solving a problem of size \(n\). Specify the complexity of each algorithm using big \(O\)-notation.
- \(500n + 100n^{1.5} + 50n \log_{10}n\)
- \(n \log_3 n + n \log_2 n\)
- \(n^2 \log_2 n + n (\log_2 n)^2\)
- \(0.5 n + 6n ^{1.5} + 2.5 \cdot n ^{1.75}\)
2.6.8. Exercise 7¶
The following statements provide some “properties” of the big O-notation for the functions \(f(n)\), \(g(n)\) etc. State whether each statement is TRUE or FALSE. If it is true, provide a proof sketch using the properties of the O-notation. If it is false, provide a counter-example, and if you a way to fix it (e.g., by changing the boundary on the right), provide a “correct” formulation a proof sketch while it holds.
- \(5 n + 10 n^2 + 100 n^3 \in O(n^4)\)
- \(5n + 10n^2 + 100 n^3 \in O(n^2 \log n)\)
- Rule of products: \(g_1 (n) \in O(f_1(n))\) and \(g_2 (n) \in O(f_2(n))\), then \(g_1 (n) \cdot g_2 (n) \in O(f_1(n) \cdot f_2(n))\).
- Prove that \(T_n = c_0 + c_1 n + c_2 n^2 + c_3 n^3 \in O(n^3)\) using the formal definition of the big \(O\) notation.
2.6.9. Exercise 8¶
One of the two software packages, A or B, should be chosen to process data collections, containing each up to \(10^{12}\) records. Average processing time of the package A is \(T_A(n) = 0.1 \cdot n \cdot \log_2 n\) nanoseconds and the average processing time of the package B is \(T_B(n) = 5 \cdot n\) nanoseconds. Which algorithm has better performance in the big \(O\) sense? Work out exact conditions when these packages outperform each other.
2.6.10. Exercise 9¶
Algorithms A and B spend exactly \(T_A(n) = c_A \cdot n \cdot \log_2 n\) and \(T_B(n) = c_B \cdot n^2\) nanoseconds, respectively, for a problem of size \(n\). Find the best algorithm for processing \(n = 2^{20}\) data items if the algorithm A spends 10 nanoseconds to process 1024 items, while the algorithm B spends only 1 nanosecond to process 1024 items.