5.2. Best-Worst Case for Comparison-Based Sorting

A strength and a weakness of Comparison-Based Sorting is the fact that the only operation it relies in its implementation is a primitive to compare two elements. This makes it very generic and applicable to diverse classes of data, but also puts a theoretical limit on how fast (in the asymptotic big-O sence) we can sort arrays if we use only comparison.

Let us se what is this theoretical limit. Quicksort, Insertion sort, Merge sort are all comparison-based sorting algorithms: they compare elements pairwise. An “ideal” algorithm will always perform no more than \(t(n)\) comparisons, for the worst possible case on an array of size \(n\). What is then \(t(n)\)?

Let us think in the following way. What a sorting delivers is a permutation of an initial array, which is also sorted. A number of possible permutations of \(n\) elements is \(n!\), and such an algorithm should find “the right one” by following a path in a binary decision tree, where each node corresponds to comparing just two elements.

As an example, consider the following decision tree for an array of just three elements [|A; B; C|]:

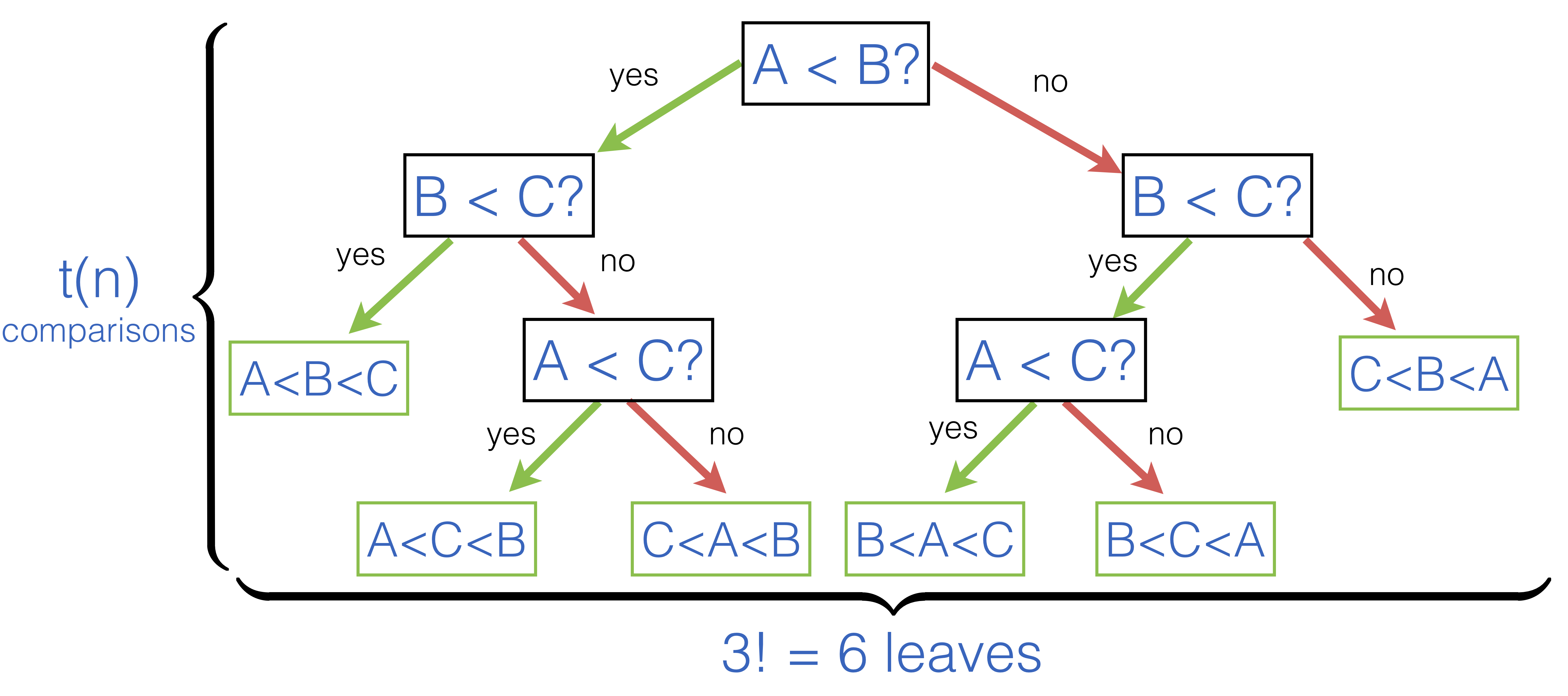
_images/decisions.png

Intuitively, by making \(t(n)\) steps in a decision tree, in its search for the “correctly ordered” permutation, the algorithm should be able to say, which ordering it is. Since the number of reachable leaves in \(t(n)\) steps is \(2^{t(n)}\), and the number of possible orderings is \(n!\), it should be the case that

\[2^{t(n)} \geq n!\]

To obtain the boundary on \(t(n)\) we need to solve this inequality. We can do so by first taking tha logarithm of the both sides:

\[t(n) \geq \log_2(n!)\]

We can then use Stirling’s formula for large \(n\), which states that \(n! \approx \sqrt{2\pi n}\left(\frac{n}{e}\right)^n\). Therefore, we obtain

\[t(n) \approx n \log_e n = (\log_e 2) n \log_2 n \in O(n \log n)\]

With this we establish that the best possible algorithm for sorting arrays using only comparison will be deemed to perform \(O(n \log n)\) comparisons in the worst case.

The complexity class \(O(n \log n)\) is so paramount in the study of algorithms that it deserved its own name: computations having this complexity are often referred to as having linearithmic complexity.