8.3. Bloom Filters and Their Applications¶
- File:
BloomFilters.ml
Hashing can be useful for other applications besides distributing elements in an array when implementing a hash-table. For instance, we can also employ hashing for compactly representing the information of whether a certain element is or is not in a given set. To do so, let us first the introduce the following notion dealing with algorithms and data structures occasionally giving “wrong” answers.
True Negatives and False Positives
Let us notice that some applications do not require to always have the correct answer to the question
“Whether the element e is in the set s”?
Imagine that we have a data structure, such that
- when the data structure answers “no” to the above question, it means “the element
eis certainly not in the sets”, but - when it answers “yes” the above question, it means that “the element
emight or might not be in sets”.
This behaviour of the data structure is typically called as “sound-but-incomplete”. The first scenario (precise no-answer) is called “true negatives”, while the case of the second scenario, in which the answer “yes” is given for a certain element not in the set is called “false positive” (if the element is in the set, it would be “true positive”).
Data structures that experience false positives, but no false negatives (the answer “no” is precise), while providing a compact representation, are very useful and are employed in applications, that might tolerate imprecise “yes”-answers, given conservatively.
In this section, we will study one of such data structures called Bloom filter — a compact representation of a “lossy” set that provides precisely this functionality. Bloom filters are widely used in practice:
- Google Chrome web browser used to use a Bloom filter to identify malicious URLs.
- Medium uses Bloom filters to avoid recommending articles a user has previously read.
- Bitcoin uses Bloom filters to speed up wallet synchronisation.
8.3.1. High-level intuition¶
Bloom filter is a very simple data structure, which uses hashing. It
is represented by a large boolean/bit array (you can think of it of an
array of 0s and 1s) of size m, and a finite number k of
different hash-functions, which map elements to be added to a set of
interest to int (as usual).
For each new element to be added to the set, all k hash functions are used to determine specific bits, corresponding to this element in the array. The combination of those positions is the element’s “image”. For instance, the following image shows a Bloom filter with m = 15 and k = 3, with an example of three elements, X, Y, and Z, added to it.
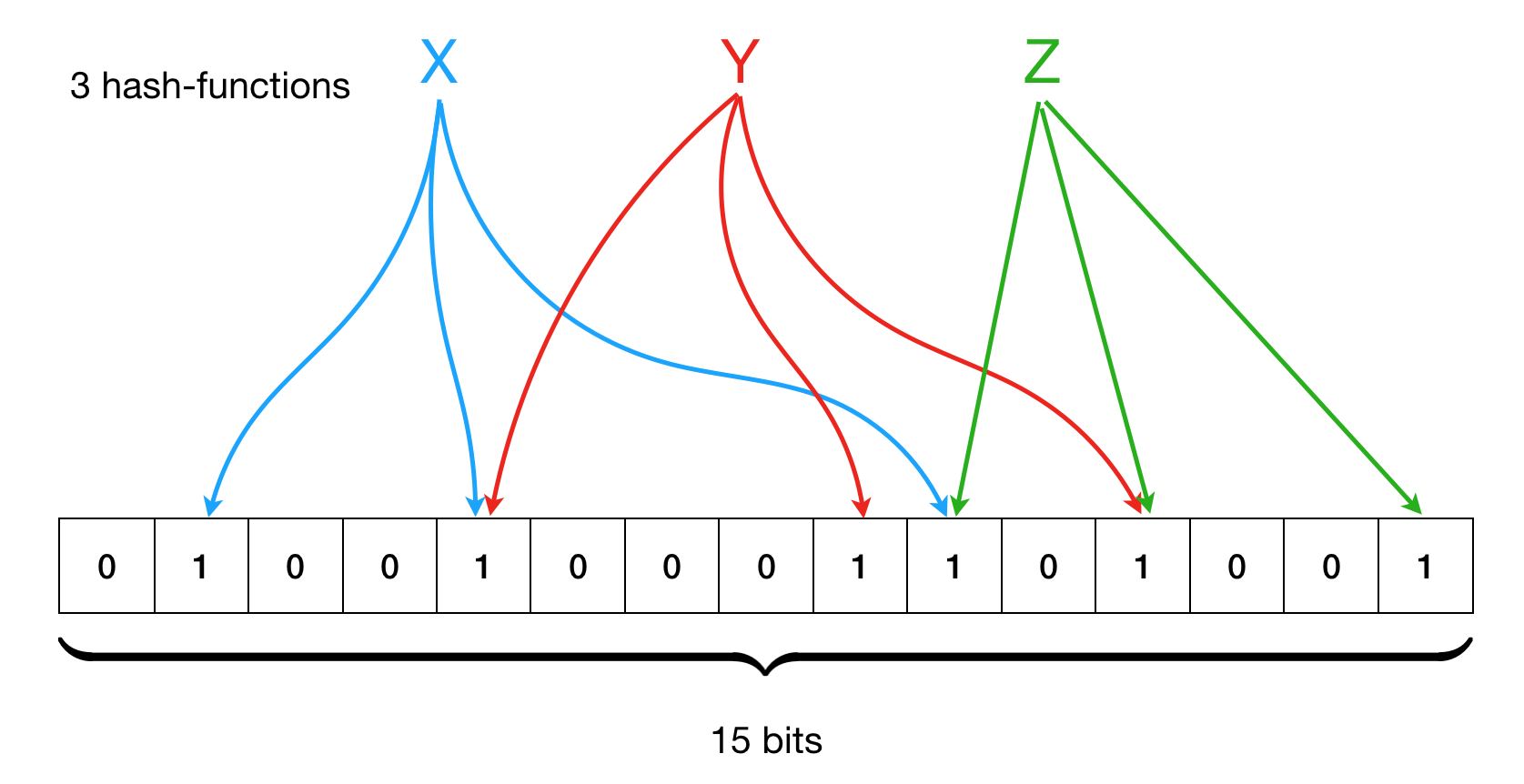
To determine whether an element is in the set, one needs to compute its k hashes, and check the bits in the corresponding array in a constant time (\(O(k)\)). Having more than 1 hash function reduces the risk of collision if the number of elements is smaller than the size of the filter, however, two or more different elements can indeed have all similar k hashes.
Elements are never removed from a Bloom filter.
8.3.2. Bloom filter signature¶
Let us first define the Bloom filter signature. It starts from the module describing the type of its elements and the list of hash functions:
module type BloomHashing = sig
type t
val hash_functions : (t -> int) list
end
The Bloom filter itself is a functor, parameterised by BloomHashing:
module type BloomFilter = functor
(H: BloomHashing) -> sig
type t
val mk_bloom_filter : int -> t
val insert : t -> H.t -> unit
val contains : t -> H.t -> bool
val print_filter : t -> unit
end
8.3.3. Implementing a Bloom filter¶
The implementation of the Bloom filter is simply an array of booleans (which we use to represent 0/1-bits) of a fixed size:
module BloomFilterImpl : BloomFilter = functor
(H: BloomHashing) -> struct
(* Type of filter *)
type t = {
slots : bool array;
size : int
}
(* Functions come here *)
end
Creation of a Bloom filter is trivial:
let mk_bloom_filter n =
let a = Array.make n false in
{slots = a; size = n}
Insertion amounts to computing all hashes for the element and setting the corresponding array bits to true:
let insert f e =
let n = f.size in
List.iter (fun hash ->
let h = (hash e) mod n in
f.slots.(h) <- true) H.hash_functions
and to check if an element is in the filter, we need to compute all its hashes and check the corresponding bits:
let contains f e =
if H.hash_functions = [] then true
else
let n = f.size in
let res = ref true in
List.iter (fun hash ->
let h = (hash e) mod n in
res := !res && f.slots.(h)) H.hash_functions;
!res
We can implement a printer for the Bloom filter by means of one of the previous modules:
module BP = ArrayPrinter(struct
type t = bool
let pp b = if b then "1" else "0"
end)
let print_filter t =
let open BP in
print_array t.slots
8.3.4. Experimenting with Bloom filters¶
Let us fix a hashing strategy for our favourite data type int * string:
module IntStringHashing = struct
type t = int * string
let hash1 (k, _) = Hashtbl.hash k
let hash2 (_, v) = Hashtbl.hash v
let hash3 (k, _) = k
let hash_functions = [hash1; hash2; hash3]
end
Instantiating the filter:
module IntStringFilter = BloomFilterImpl(IntStringHashing)
Filling a filter from an array:
let fill_bloom_filter m n =
let open IntStringFilter in
let filter = mk_bloom_filter m in
let a = generate_key_value_array n in
for i = 0 to n - 1 do
insert filter a.(i)
done;
(filter, a)
Let’s do some experiments:
utop # let (f, a) = fill_bloom_filter 20 10;;
val f : IntStringFilter.t = <abstr>
val a : (int * string) array =
[|(4, "ayuys"); (7, "cdrhf"); (4, "ukobi"); (5, "hwsjs"); (8, "uyrla");
(0, "uldju"); (3, "rkolw"); (7, "gnzzo"); (7, "nksfe"); (4, "geevu")|]
utop # IntStringFilter.contains f (3, "rkolw");;
- : bool = true
utop # IntStringFilter.contains f (13, "aaa");;
- : bool = false
utop # IntStringFilter.print_filter f;;
[| 1; 0; 0; 1; 1; 1; 0; 1; 1; 1; 1; 0; 1; 0; 1; 1; 0; 1; 1; 0 |] - : unit = ()
8.3.5. Testing Bloom Filters¶
Testing for no true positive:
let%test "bloom filter true positives" =
let open IntStringFilter in
let fsize = 2000 in
let len = 1000 in
let (f, a) = fill_bloom_filter fsize len in
for i = 0 to len - 1 do
assert (contains f a.(i))
done;
true
Testing for true negatives:
let%test "bloom filter true negatives" =
let open IntStringFilter in
let fsize = 2000 in
let len = 1000 in
let (f, a) = fill_bloom_filter fsize len in
let al = array_to_list 0 len a in
let b = generate_key_value_array len in
for i = 0 to len - 1 do
let e = b.(i) in
if (not (contains f e))
then assert (not (List.mem e al))
done;
true
However, there can be also false positives, although we don’t check for them.
8.3.6. Improving Simple Hash-table with a Bloom filter¶
Let us put Bloom filter to some good use by improving our simple implementation of a hash table.
The way we implemented hash-tables before made them waster too much on iterating through the buckets before adding or getting an element. This is something that can be improved with a Bloom filter: indeed if we known that there is no element with a certain key in the bucket (the answer that Bloom filter can answer precisely), we don’t have to look for it.
The price to pay for this speed-up is inability to remove elements from the hash-table (as one cannot remove elements from a Bloom filter).
We start our hash-table from the following preamble. Its core data structure now gets enhanced with a Bloom filter:
module BloomHashTable (K: BloomHashing) = struct
type key = K.t
(* Adding bloom filter *)
module BF = BloomFilterImpl(K)
type 'v hash_table = {
buckets : 'v list array;
capacity : int;
filter : BF.t
}
(* Functions come here *)
end
For simplicity, upon creating a hash table, we make a Bloom filter with a fixed capacity:
let mk_new_table cap =
let buckets = Array.make cap [] in
(* Pick reasonably large BF size *)
let filter = BF.mk_bloom_filter 15000 in
{buckets = buckets;
capacity = cap;
filter = filter}
Insertion also updates the filter correspondingly:
let insert ht k v =
let hs = Hashtbl.hash k in
let bnum = hs mod ht.capacity in
let bucket = ht.buckets.(bnum) in
let filter = ht.filter in
let clean_bucket =
(* New stuff *)
if BF.contains filter k
(* Only filter if ostensibly contains key *)
then List.filter (fun (k', _) -> k' <> k) bucket
else bucket in
(* Missed in the initial the implementation *)
BF.insert filter k;
ht.buckets.(bnum) <- (k, v) :: clean_bucket
Fetching consults the filter first:
let get ht k =
let filter = ht.filter in
if BF.contains filter k then
let hs = Hashtbl.hash k in
let bnum = hs mod ht.capacity in
let bucket = ht.buckets.(bnum) in
let res = List.find_opt (fun (k', _) -> k' = k) bucket in
match res with
| Some (_, v) -> Some v
| _ -> None
else None
As announced before, removal is prohibited:
let remove _ _ = raise (Failure "Removal is deprecated!")
8.3.7. Comparing performance¶
Let us instantiate the Bloom filter-enhanced hash table:
module BHT = BloomHashTable(IntStringHashing)
module BHTTester = HashTableTester(BHT)
Similarly to methods for testing performance of previously defined hash-tables, we implement the following function:
let insert_and_get_bulk_bloom a m =
Printf.printf "Creating Bloom hash table:\n";
let ht = time (BHTTester.mk_test_table_from_array_length a) m in
Printf.printf "Fetching from Bloom hash table on the array of size %d:\n" (Array.length a);
let _ = time BHTTester.test_table_get ht a in ()
Now, let us compare the Bloom filter-powered simple table versus vanilla simple hash-table:
let compare_hashing_time_simple_bloom n m =
let a = generate_key_value_array n in
insert_and_get_bulk_simple a m;
print_endline "";
insert_and_get_bulk_bloom a m
Running the experiments, we observe not so much gain when a number of elements and the buckets are in the same ballpark:
utop # compare_hashing_time_simple_bloom 10000 5000;;
Creating simple hash table:
Execution elapsed time: 0.003352 sec
Fetching from simple hash table on the array of size 10000:
Execution elapsed time: 0.000001 sec
Creating Bloom hash table:
Execution elapsed time: 0.007994 sec
Fetching from Bloom hash table on the array of size 10000:
Execution elapsed time: 0.000001 sec
However, the difference is noticeable when the number of buckets is small, and the sie of the filter is still comparable with the number of elements being inserted:
utop # compare_hashing_time_simple_bloom 15000 20;;
Creating simple hash table:
Execution elapsed time: 0.370876 sec
Fetching from simple hash table on the array of size 15000:
Execution elapsed time: 0.000002 sec
Creating Bloom hash table:
Execution elapsed time: 0.234405 sec
Fetching from Bloom hash table on the array of size 15000:
Execution elapsed time: 0.000000 sec