12.1. Representing Sets via Binary Search Trees¶
- File
BST.ml
Binary Search Trees (BSTs) are one of the most versatile representations of mutable sets of ordered elements, supporting a variety of operations, such as insertion, deletion, checking membership, finding minimums, maximums, predecessors and successors of a value — all those operations taking the time proportional to the height \(h\) of the tree or, if the tree is constructed randomly out of \(n\) elements — \(O(\log n)\). This makes BST a superior alternative to lists, heaps, and even hash-tables when impelmenting mutable sets with a number of standard set operations.
The key to this expressivity and efficience is the invariant of a
tree-shaped data structure, that mandates that, for any node q,
- any element in its left subtree
q.lis less or equal (with respect to a certain total order) than the element in the nodeqitself, and - any element in its right subtree
q.ris greater or equal than the element in the nodeqitself.
This invariant is maintained by all operations that modify the set, and is relied upon by all its queries. The logarithmic complexity of operations, thus, follows from the intuition similar to the one powering Binary Search in arrays.
12.1.1. A Data Structure for Binary-Search Trees¶
We start by defining a linked in-memory data structure for BSTs in its own module.
The tree is populated by nodes, each of which carries a value (immutable), and also maintains references (mutable) to its left/right children and a parent, which can be either absent or refer to some other nodes of the tree:
module BinarySearchTree = struct
type 'e tree_node = {
value : 'e;
parent : 'e tree_node option ref;
left : 'e tree_node option ref;
right : 'e tree_node option ref;
}
type 'e tree = {
root : 'e tree_node option ref;
size : int ref
}
(* More definitions coming here *)
end
For convenience, we define several operations to dereference various components of a tree and its nodes:
let left n = !(n.left)
let right n = !(n.right)
let parent n = !(n.parent)
let get_root t = !(t.root)
let get_size t = !(t.size)
let mk_node e =
{value = e;
parent = ref None;
left = ref None;
right = ref None}
let mk_tree _ = {root = ref None; size = ref 0}
Finally, since nodes are represented by an option type, we introduce the following combinator, simplifying working with option-wrapped values:
let map_option o f z = match o with
| None -> z
| Some n -> f n
In words map_option returns applies f to the value n within o, if o = Some n, or returns z otherwise.
12.1.2. Inserting an element into a BST¶
The defined above mk_tree function creates an empty tree. Let us now implement a procedure for populating it with elements by inserting them one by one:
let insert t e =
let rec insert_element n e =
let m = mk_node e in
if e < n.value
then match left n with
| Some m -> insert_element m e
| None ->
m.parent := Some n;
n.left := Some m;
true
else if e > n.value
then match right n with
| Some m -> insert_element m e
| None ->
m.parent := Some n;
n.right := Some m;
true
else false
in
match !(t.root) with
| None -> (
t.root := Some (mk_node e);
t.size := 1;
true)
| Some n ->
if insert_element n e
then (t.size := !(t.size) + 1; true)
else false
Notice that the main working routine insert_element respects the
BST property defined above: it positions the node m with the
element e, so it would be in the correct subtree
(smaller-left/greater-right) with respect to its parent nodes.
Finally, insert_element returns a boolean to indicate whether the
element has been indeed added (true) or ignored as duplicated
(false). In the former case the size of the tree is increased, in
the latter it remains the same.
12.1.3. Binary-Search-Tree Invariant¶
Let us now assert that tree-manipulating operations such as insert
indeed preserve the discussed above BST property. For this, let us
define the BST invariant in the form of the following function:
let check_bst_inv t =
let rec walk node p =
(p node.value) &&
let res_left = match left node with
| None -> true
| Some l -> walk l (fun w -> p w && w <= node.value)
in
let res_right = match right node with
| None -> true
| Some r -> walk r (fun w -> p w && w >= node.value)
in
res_left && res_right
in
match !(t.root) with
| None -> true
| Some n -> walk n (fun _ -> true)
The main recursive sub-function walk works by “growing” a predicate p that applies to each node further down the tree, making sure that it is correctly positioned with regard to all its parents. At the top level p is instantiated with (fun _ -> true), as there are no restrictions imposed for the root of the tree, but more and more conjuncts added, as the checking proceeds recursively.
12.1.4. Testing Tree Operations¶
Let us put or invariant to work by using it to test the correctness of insert.
We do so by first defining a function for generating random trees from random arrays via insertion:
open BinarySearchTree
let mk_tree_of_size n =
let t = mk_tree () in
let a = generate_key_value_array n in
for i = 0 to n - 1 do
insert t a.(i)
done;
t
Next, we check that the generated trees indeed satisfy the BST property:
let%test "Testing insertion" =
let n = 1000 in
let t = mk_tree_of_size n in
check_bst_inv t
12.1.5. Printing a Tree¶
It would be very nice if we could not only test but also visualise our binary search trees.
Unfortunately, printing a tree in a standard top-down fashion requires quite a bit of book-keeping of tree-specific information. Printing a tree left-to-right is, however, can be done quite easily as follows:
let print_tree pp snum t =
let print_node_with_spaces l s =
for i = 0 to s - 1 do
Printf.printf " "
done;
print_endline (pp l.value);
in
let rec walk s node = match node with
| None -> ()
| Some n -> begin
walk (s + snum) (right n);
print_node_with_spaces n s;
walk (s + snum) (left n);
end
in
map_option (get_root t) (fun n -> walk 0 (Some n)) ()
The first auxiliary function print_node_with_spaces prints a string of s spaces and the value of a node l.
The second function walk traverses the tree recursively, accumulating the “offset” proportionally to the depth of the tree node. It first prints the right sub-tree, then the node itself and then the left sub-tree, making use of the accumulated offset for printing the necessary number of spaces. Finally, it runs walk for the top-level root node, if it exists.
Let us observe the effect of print_tree by instantiating it to print trees of key-value pairs:
let print_kv_tree = print_tree
(fun (k, v) -> Printf.sprintf "(%d, %s)" k v) 12
We can now use utop to experiment with it:
utop # open BST;;
utop # open BinarySearchTree;;
utop # let t = mk_tree ();;
val t : '_weak1 tree = {root = {contents = None}}
utop # let a =
[|(4, "ayuys"); (7, "cdrhf"); (4, "ukobi"); (5, "hwsjs"); (8, "uyrla");
(0, "uldju"); (3, "rkolw"); (7, "gnzzo"); (7, "nksfe"); (4, "geevu")|]
utop # for i = 0 to 9 do insert t a.(i) done;;
- : unit = ()
utop # print_kv_tree t;;
(8, uyrla)
(7, nksfe)
(7, gnzzo)
(7, cdrhf)
(5, hwsjs)
(4, ukobi)
(4, geevu)
(4, ayuys)
(3, rkolw)
(0, uldju)
- : unit = ()
That is, on can see that (4, "ayuys") is the root of the tree, and the whole structure satisfies the BST property.
12.1.6. Searching Elements¶
We define the search function so it would return not just the element, but also the node that contains it. It does so by recursively traversing the tree, while relying on its BST property:
let search t k =
let rec walk k n =
let nk = n.value in
if k = nk then Some n
else if k < nk
then match left n with
| None -> None
| Some l -> walk k l
else match right n with
| None -> None
| Some r -> walk k r
in
map_option (get_root t) (walk k) None
In the absence of the abstract module signature, it is quite dangerous to return a node (not just its value), as one can break the BST properties, by messing with its mutable components (e.g., reference to left/right children). However, returning a node also simplifies the implementation of various testing and manipulation procedures, specifically, deletion of tree nodes.
12.1.7. Tree Traversals¶
There are multiple ways to flatten a tree into a list, which can be convenient for the sake of testing and other inspections.
The simplest way to do it is via an accumulator (implemented as a mutable queue) and a procedure, known as Depth-First-Search (DFS), which traverses the tree recursively, following its order (sometimes, this travelsal is also called in-order traversal):
open Queues
open DLLBasedQueue
let depth_first_search_rec t =
let rec walk q n =
(match left n with
| Some l -> walk q l
| None -> ());
enqueue q n.value;
(match right n with
| Some r -> walk q r
| None -> ());
in
let acc = (mk_queue 0) in
map_option (get_root t) (walk acc) ();
queue_to_list acc
With the call stack, DFS traverses the tree in a Last-In-First-Out mode (LIFO). By replacing the implicit stack with an explicit mutable queue (First-In-First-Out, FIFO), we can obtain an alternative traversal, known as Breadth-First-Search (BFS), so it would accumulate tree elements by following its “layers”:
let breadth_first_search_loop t =
let loop wlist q depth =
while not (is_empty wlist) do
let n = get_exn @@ dequeue wlist in
(match left n with
| Some l -> enqueue wlist l
| _ -> ());
enqueue q n.value;
(match right n with
| Some r -> enqueue wlist r
| _ -> ());
done
in
let acc = (mk_queue 0) in
let wlist = mk_queue 0 in
(match get_root t with
| None -> ()
| Some n -> begin
enqueue wlist n;
loop wlist acc 0;
end);
queue_to_list acc
We can also define all elements of the set in terms of the traversal:
let elements t = breadth_first_search_loop t
12.1.8. Testing Element Retrieval and Tree Traversals¶
As we know well how to work with lists, we can use traversals to test each other, as well as the search function:
(******************************************)
(* Testing traversals *)
(******************************************)
let check_elem_in_tree t e =
let n = search t e in
(get_exn @@ n).value = e
let%test "Testing DFS" =
let n = 1000 in
let t = mk_tree_of_size n in
let l1 = depth_first_search_rec t in
List.length l1 = n &&
List.for_all (fun e -> check_elem_in_tree t e) l1 &&
sorted l1
let%test "Testing BFS" =
let n = 1000 in
let t = mk_tree_of_size n in
let l1 = depth_first_search_rec t in
let l2 = breadth_first_search_loop t in
List.length l1 = n &&
List.for_all (fun e -> List.mem e l2) l1 &&
List.for_all (fun e -> List.mem e l1) l2
(******************************************)
(* Testing retrieval *)
(******************************************)
let%test "Testing retrieval" =
let n = 1000 in
let t = mk_tree_of_size n in
let m = Random.int n in
let l = breadth_first_search_loop t in
let e = List.nth l m in
let z = search t e in
z <> None
12.1.9. More BST operations¶
Thanks to its invariant, a BST makes it almost trivial to implement operations, such as
- Getting minimum/maximum element in a set representing by a tree
- Find a successor/predecessor of an element
For instance, finding the minimal element of a subtree starting from a node
n can be achieved by the following operation:
let rec find_min_node n =
match left n with
| Some m -> find_min_node m
| None -> n
Notice that this operation does not find the global tree-wise successor of the element in node n, although that is also possible to do in \(O(\log n)\) operations for a tree that is well-balanced (i.e., not to “tall” and “thin”).
12.1.10. Deleting a node from BST¶
Deletion of a node from a BST is the most complicated operation, as it requires significant restructuring of the tree in order to maintain its invariant.
Deletion of a non-leaf node from a tree will require some other node (along with its subtree) to take its place. This can be achieved by the following operation for performing “transplantation” of one node by another:
(* Replacing node U by (optional) node V in T. *)
let transplant t u v =
(match parent u with
| None -> t.root := v
| Some p ->
match left p with
| Some l when u == l -> p.left := v
| _ -> p.right := v);
(* Update parent of v *)
match v with
| Some n -> n.parent := parent u
| _ -> ()
Notice the comparison via when u == l in the implementation above.
This is essential: node references must be compared using OCaml’s
“shallow” equality mechanism, as structural “deep” equality on
references (=) in the case of linked data structures, such as
BSTs, may lead to errors that are very difficult to debug.
Let us now discuss possible scenarios for removing a node z from the tree T by preserving the BST property.
- The simplest case is when
zis a leaf, so we can simply remove it. - The node
zhas no left child. In this case, we can simply replace it by its right child (argue, why this is correct) as on the picture below:
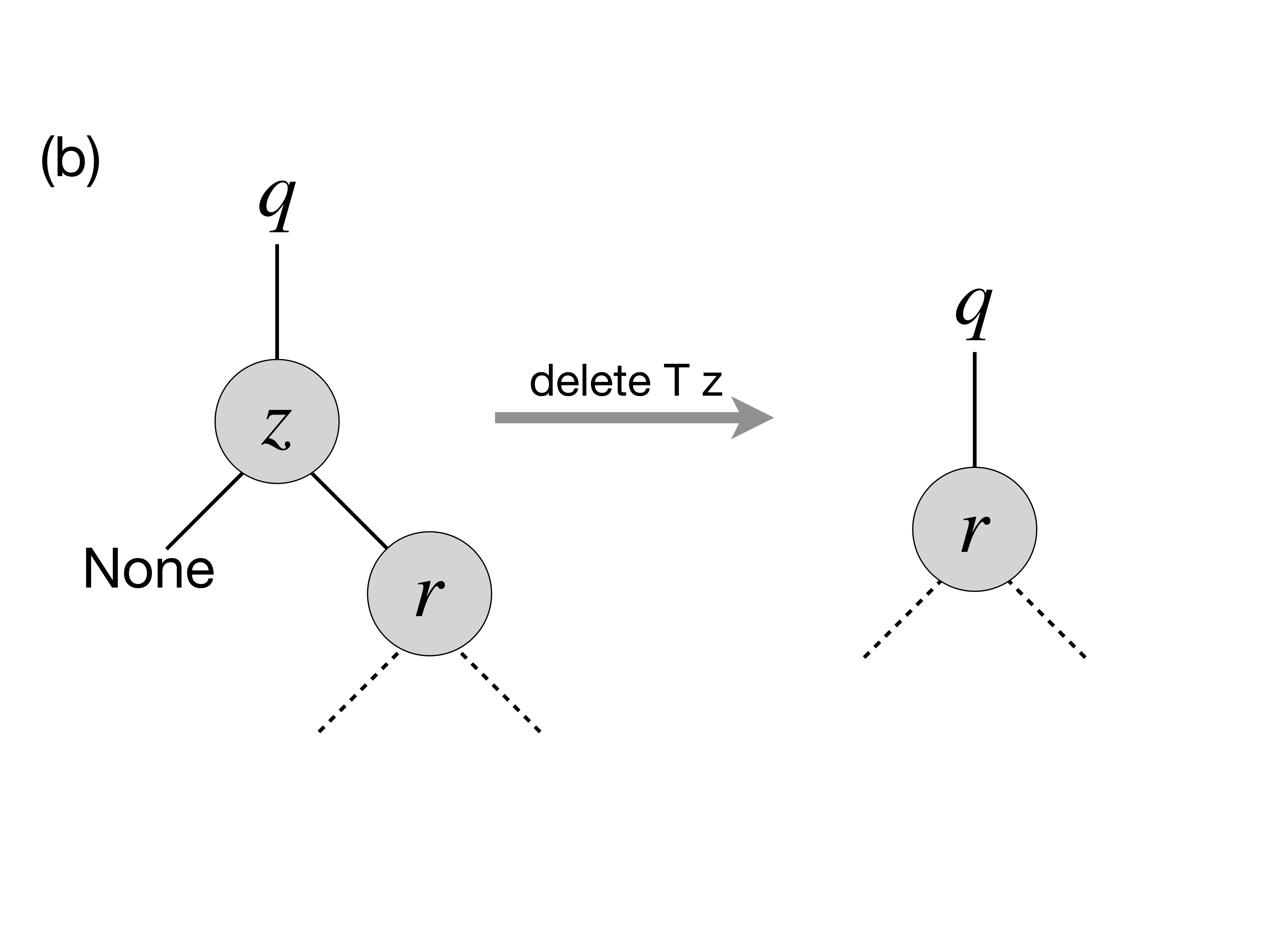
- A similar situation takes place when
zhas only the left child, which replaces it (viatransplant):
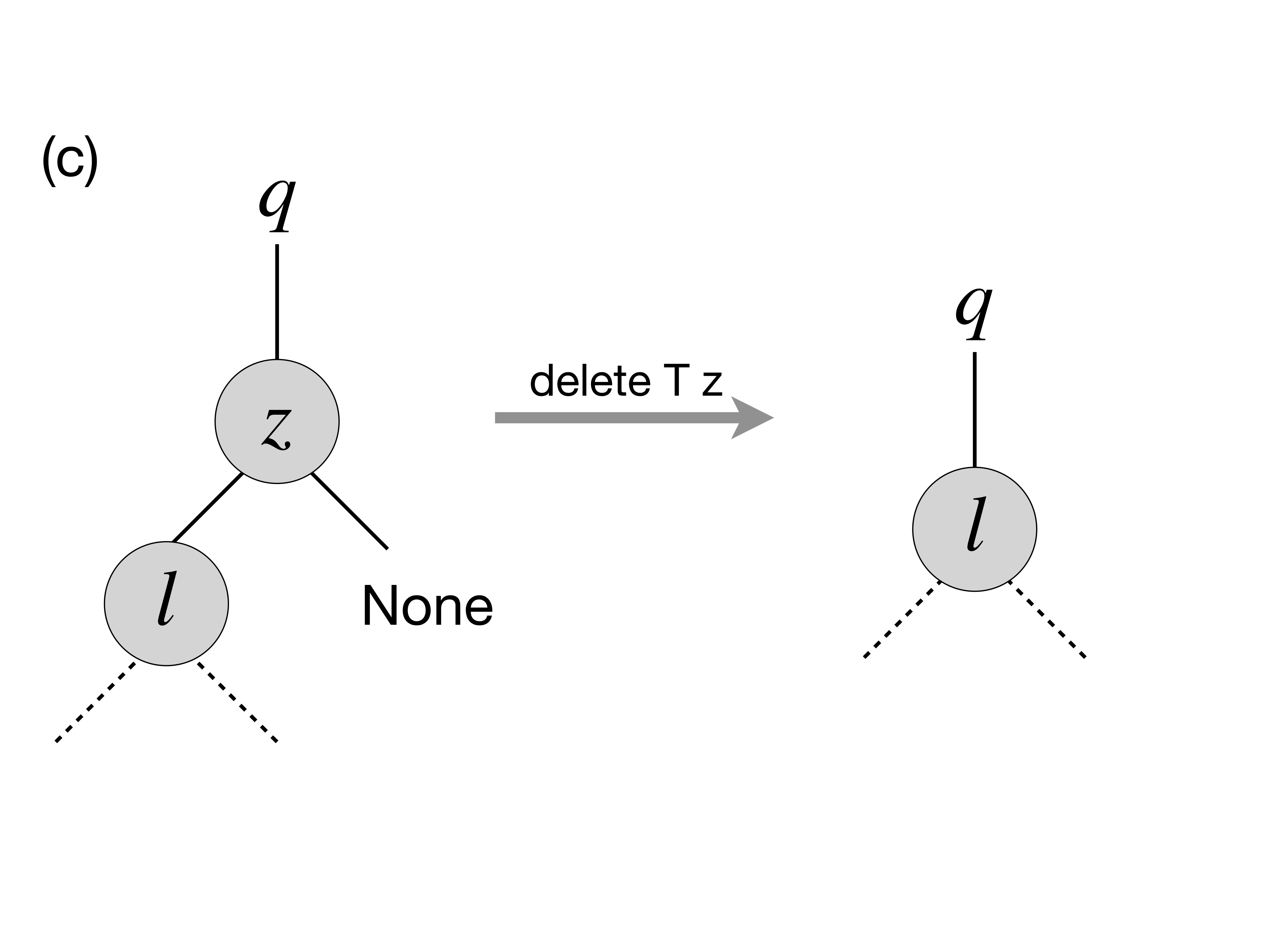
- In the case when
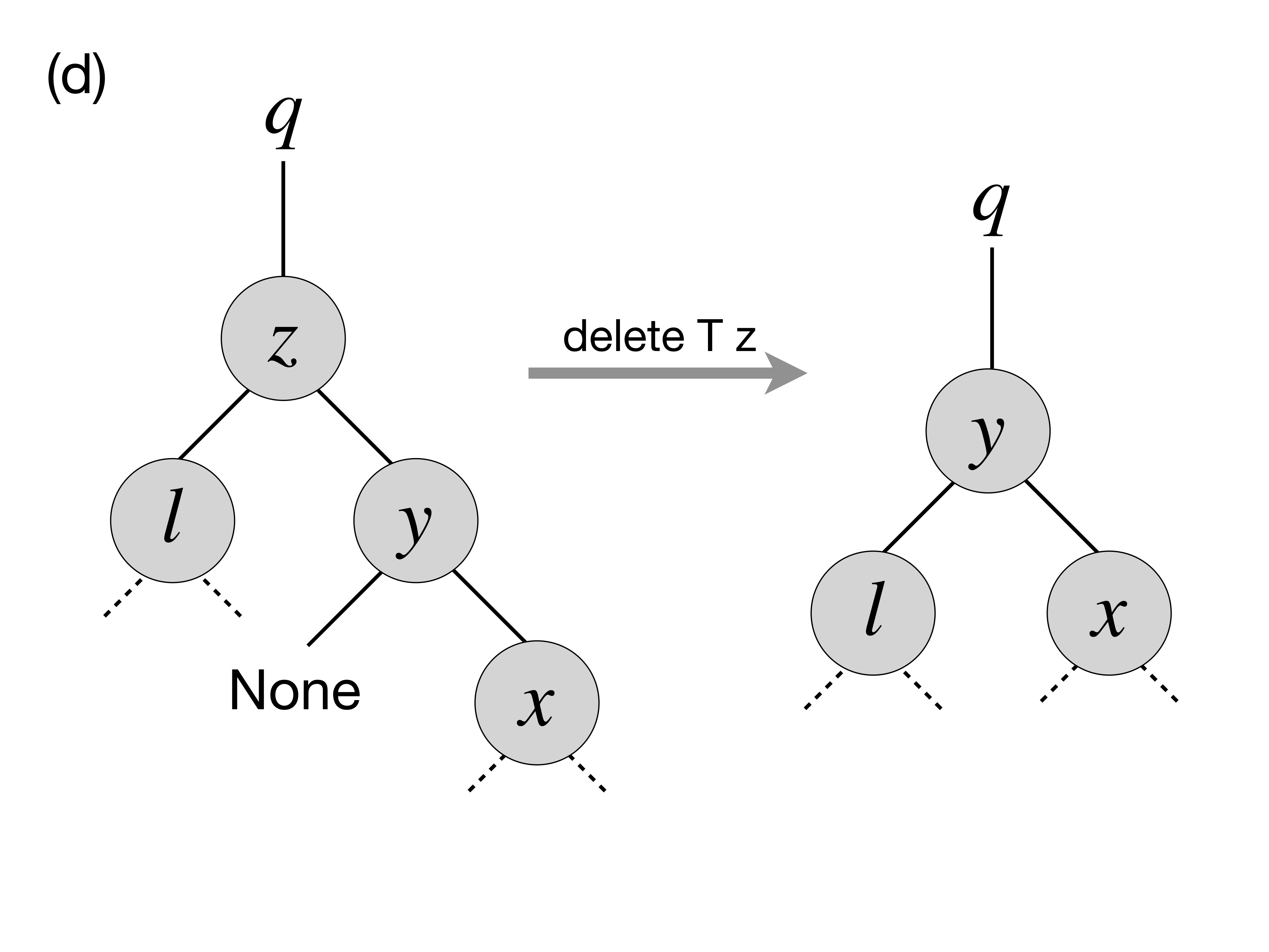
zhas two children, we need to look up for the node that corresponds to its successor inz-rooted subtree wrt. the ordering of elements. In this particular case, such a successor,y, is the immediate right child ofzthat has no left child itself (convince yourself that in this caseyis indeed a successor ofz), therefore we can transplateyto replacez:
- Finally, in the most nasty case,
y, the successor ofz(in its subtree), is buried deep belowz, and potentially hasa right child (but no left child, otherwise it wouldn’t be the successor ofz) . In this case we need to make to perform the transformation as follows:
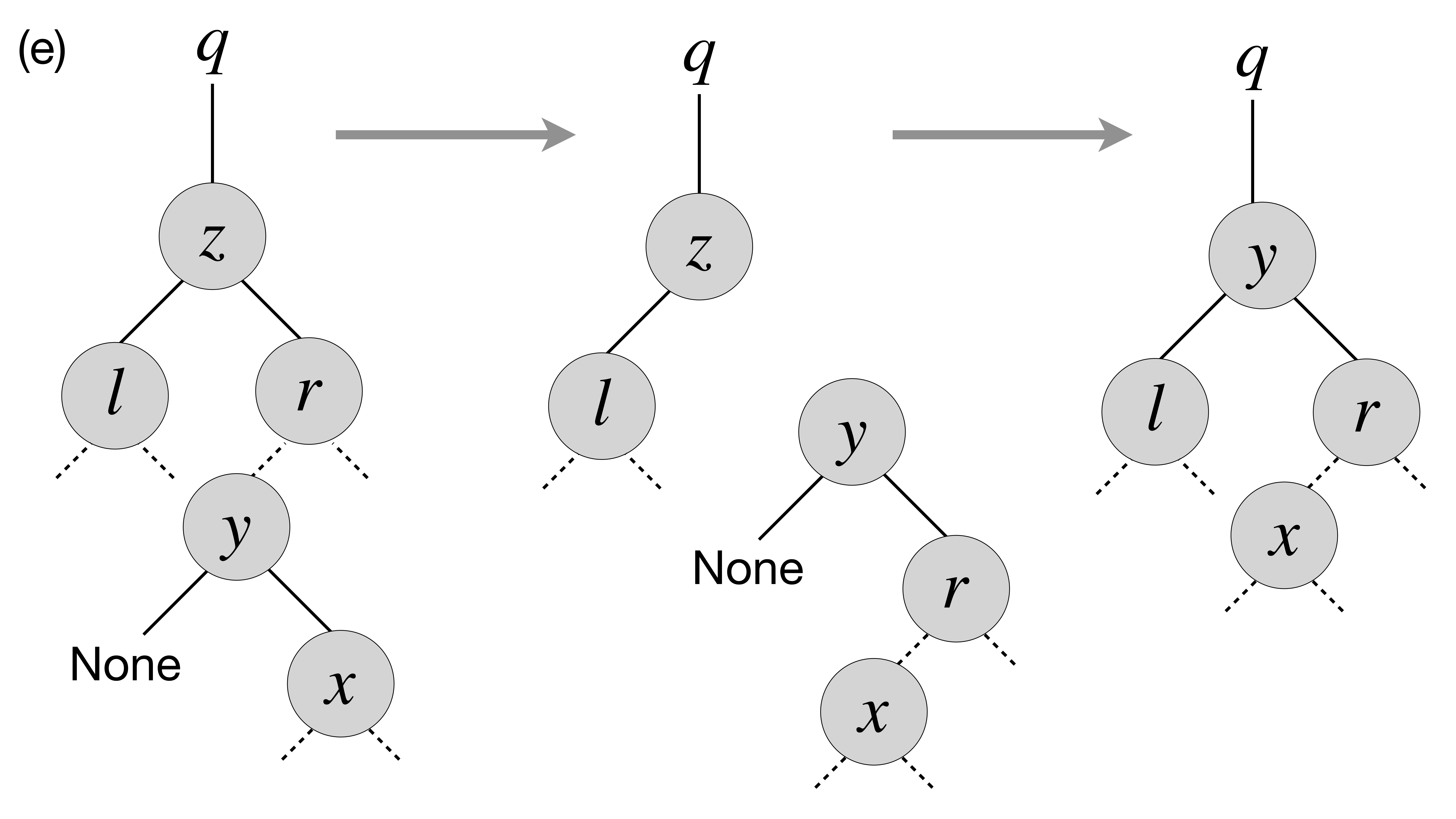
Specifically, in the last case we first transplant y with its right
child x and then make r, the former right child of z to be
the right child of y. After that we simply transplant y to the
place of z.
The full code of deletion is as follows:
let delete_node t z =
t.size := !(t.size) - 1;
if left z = None
then transplant t z (right z)
else if right z = None
then transplant t z (left z)
else
(* Finding the successor of `z` *)
let z_right_child = (get_exn @@ right z) in
let y = find_min_node z_right_child in
(* Fact: `y` has no left child *)
(if parent y <> None &&
z != get_exn @@ parent y
then
(* If y is not immediately under z,
replace y by its right subtree *)
let x = right y in
(transplant t y x;
y.right := right z;
(get_exn @@ right y).parent := Some y));
(* Now `y` replaces `z` at its position *)
transplant t z (Some y);
y.left := !(z.left);
(get_exn @@ left y).parent := Some y
How would we test deletion? We can do so by generating a random BST,
choosing a random node in it z, and then checking the following
properties for the modified tree after the deletion of z:
- The tree still satisfies the BST invariant;
- It has the previous number of elements minus one;
- All elements from the modified tree plus the deleted one are the elements of the old tree.
These checks can be automatically performed by the following function, parameterised by the size of the tree:
let test_delete n =
let t = mk_tree_of_size n in
let m = Random.int n in
let l = breadth_first_search_loop t in
let e = List.nth l m in
let z = get_exn @@ search t e in
delete_node t z;
(* Checkign the tree invariant *)
assert (check_bst_inv t);
(* Checkign the tree size *)
let ld = breadth_first_search_loop t in
assert (List.length ld = n - 1);
(* Checking integrity *)
assert (List.for_all (fun x -> List.mem x ld || x == e) l)
12.1.11. BST Rotations¶
In a BST, left and right rotations exchange the node with its right/left child (if present), correspondingly. Diagrammatically, this can be represented by the following picture:
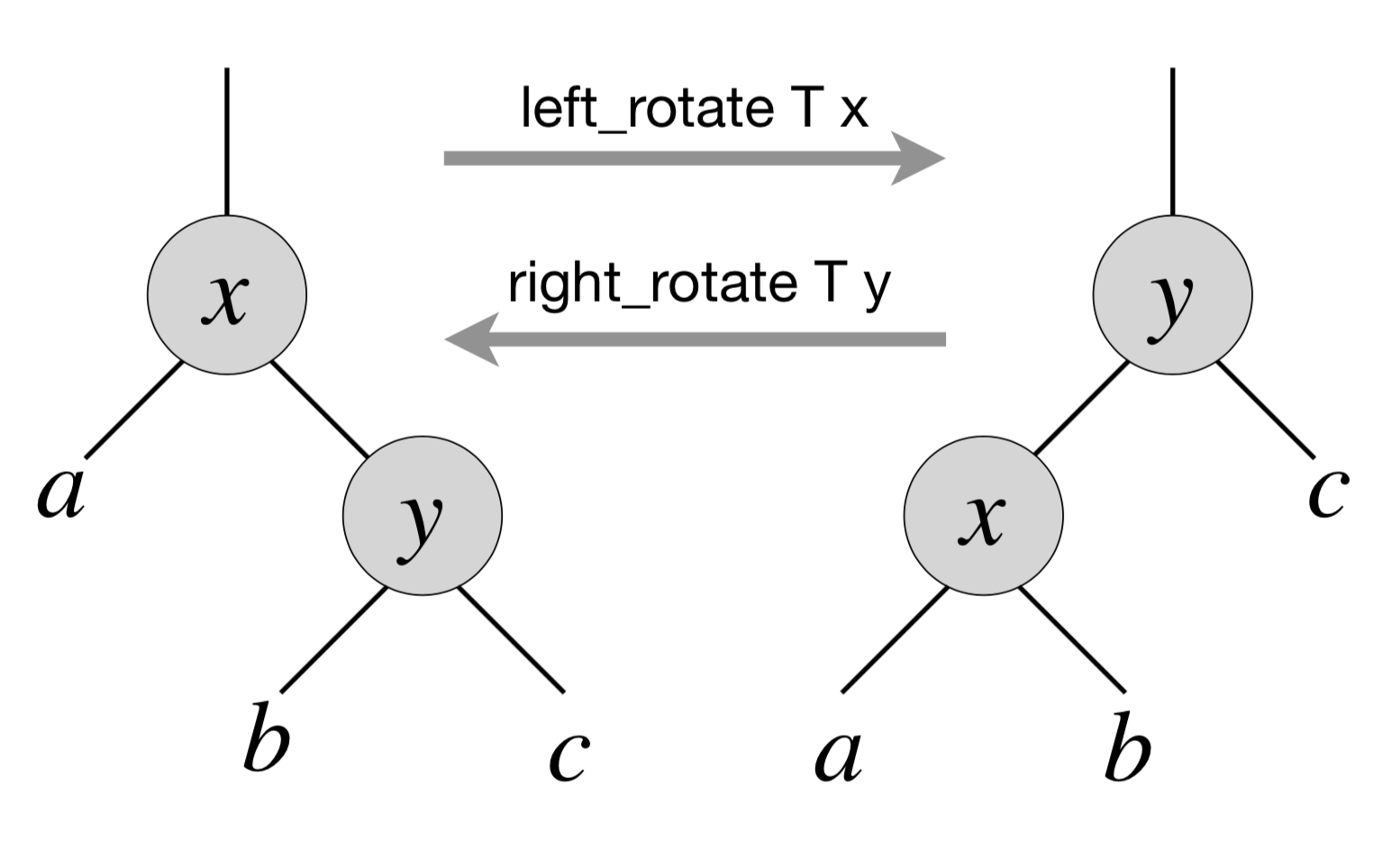
That is, via left rotation, \(y\) becomes a parent of \(x\) and vice versa. The implementation of left rotation of a node \(x\) in a tree \(T\) is given below:
let left_rotate t x =
match right x with
| None -> ()
| Some y ->
(* turn y's left subtree into x's right subtree *)
x.right := left y;
(if left y <> None
then (get_exn @@ left y).parent := Some x);
(* link x's parent to y *)
y.parent := parent x;
(match parent x with
| None -> t.root := Some y
| Some p -> match left p with
| Some l when x == l ->
p.left := Some y
| _ ->
p.right := Some y);
(* Make x the left child of y *)
y.left := Some x;
x.parent := Some y
When a subtree is rotated, the subtree side upon which it is rotated increases its height by one node while the other subtree decreases its height. This makes tree rotations useful for rebalancing a tree when it becomes “degenerate” (tall and thin). This makes it possible to keep the worst-case complexity of tree operations within \(O(\log n)\), without it degenerating to \(O(n)\).
Implementation of the right BST rotation and rotation testing of the rotations are left as an exercise.